Set

Abstract

---

• A unordered collection of Object
• Order and duplicates don’t matter

$$\{9,8,7\}=7,9,8=7,8,7,9,9,7,7$$

Notations

---

Set-Roster Notation

• A Set may be specified by writing all of its Object between braces
• Symbol ... is called ellipsis and read “and so forth”

$$\{1,2,3\}$$ $$\{1,2,3,\dots ,100\}$$ $$\{1,2,3,\dots \}$$

Set-Builder Notation

$$\{x\in U:P(x)\}$$ $$\{x\in U|P(x)\}$$

• The set of all x in U such that P(x) is true

Replacement Notation

$$\{t(x):x\in A\}$$ $$\{t(x)|x\in A\}$$

• For elements x in A, we apply the function t(x)

Properties

---

Membership of a Set

$$\in ,\notin$$ $$b\in a,b,c$$

Cardinality of a Set

$$|\{a,b,c\}|=3$$

• The size of the Set

Types of Sets

---

Subset

$$A\subseteq B\leftrightarrow \forall x(x\in A\wedge x\in B)$$

Superset

$$B\supseteq A$$

• A is a Subset of B

Proper Subset

$$A⊊B\leftrightarrow (A\subseteq B)\wedge (A\ne B)$$

Empty Set

$$\varnothing$$ $$\{\}$$ $$\varnothing \notin \{\}$$ $$\varnothing \subseteq \{\}$$

• A Set that contains 0 Object
• Itself is a Object

Null Set

Theorem 6.2.4

• An Empty Set is a s Subset of every Set
• Assume A is all the possible sets

$$\varnothing \subseteq A$$

• Proved using Vacuous Truth of Universal

Singleton

• A Set with exactly one Object

Disjoin Set

• Given 2 Set, both dont have any elements in common

$$A\cap B=\varnothing$$

Mutually Disjoin

• Also known as Pairwise Disjoint or Non-overlapping

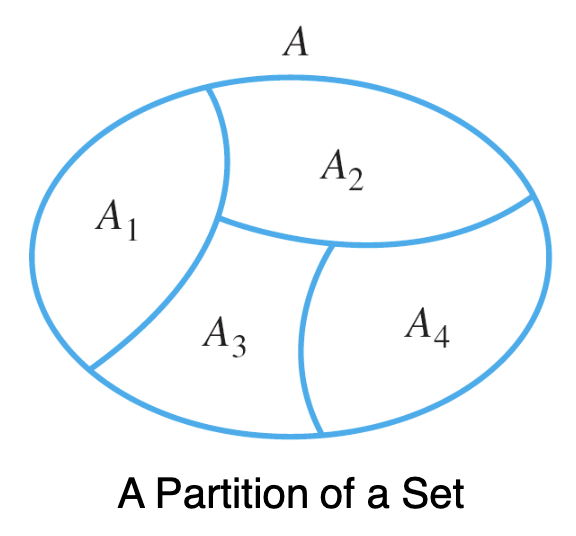
• A1, A2, A3, A4 are Mutually Disjoin
• A is called Union of Mutually Disjoint Subsets
• The collection of sets $\{A1,A2,A3,A4\}$ is said to be a Partition of A

Partition

• A partition of Set $A$ is a finite or infinite collection of noempty, Mutually Disjoin Subset that can be chained with OR to form $A$

$$\forall x\in A\exists !S\in \zeta (x\in S)$$

• $S$ is one of the mutually disjoin subset, also known as component of the partition
• $\zeta$ is the partition
• So basically each $S$ isn’t empty, and its elements are not in other mutually disjoin subset

Subset can contain duplicate elements

Given a set $A=\{a,b,c,d,e,f\}$ ,

$\{\{a\},\{b,f,b\},\{c,e,d,e\}\}$ is a valid partition

Theorem 8.3.1

• Relation induced by Partition

• Two elements are related if and only if they belong to the Mutually Disjoin Subnet in the partition. This connection created by the partition is called the relation induced by the partition

  
  

• Let $A$ be a Set with a Partition

• Let $R$ be the relation induced by the partition

• Then $R$ is Reflexive, Symmetric and Transitive

  
  

• For example, imagine dividing students in a class into groups based on their favorite sport. The relation induced by this partition would tell us which students share the same sports preference

Power Set

• The power set of Set A is all the Subset of A

$$A=\{x,y\}$$ $$\mathcal{P}(A)=\{\varnothing ,\{x\},\{y\},\{x,y\}\}$$

Theorem 6.3.1

• The cardinality of Superset of finite set is 2 to the power of the cardinality of the finite set

Theorems

---

Theorem 6.2.1

Inclusion of Intersection

$$A\cap B\subseteq A$$ $$A\cap B\subseteq B$$

Inclusion in Union

$$A\subseteq A\cup B$$ $$B\subseteq A\cup B$$

Transitive Property of Subsets

$$(A\subseteq B)\wedge (B\subseteq C)\to A\subseteq C$$

Theorem 6.2.2

• Set Identities
• Very similar to Theorem 2.1.1
• Refer to lecture 5.2.2 for more details

Terminologies

---

Object

• Members or elements of Set
• Example: 1, 2, 3 {1} are objects in the set of Integer (整数)
• It can be either a value or a set

Set Equality

• Given Set A and B. The Cardinality of a Set must be the same
• First way to prove:

$$A=B\leftrightarrow (A\subseteq B)\wedge (B\subseteq A)$$

• Second way to prove:

$$A=B\leftrightarrow \forall x(x\in A\leftrightarrow x\in B)$$

Ordered Pair

$$(c,y)$$ $$(a,b)=(c,d)\leftrightarrow (a=c)\wedge (b=d)$$

Order n-tuples

• n denotes the number of Set we are multiplying
• Ordered Pair is order 2-tuples, because are multiplying 2 sets

Cartesian Product

• Given Set A and B, the Cartesian product is a set of Ordered Pair

$$A\times B=\{(a,b):a\in A\wedge b\in B\}$$

• Thus

$$A\times B\ne B\times A$$

• Cartesian Product of real numbers is basically a set that contains all the possible (x,y) coordinates on the Cartesian Plane
• Depends on the number of set - n, the Cartesian product is a set of Order n-tuples